Revolutionizing Math Learning
For decades, mathematics education has swung between two extremes: procedural memorization for quick computation and deep conceptual understanding (National Research Council, 2001). Too often, classrooms have been forced to choose between accuracy and meaning, speed and reasoning.
But learning is not one-dimensional.
Hattie and Donoghue (2016) suggest that effective instruction depends on the intended outcome. If the goal is retention of accurate detail — surface learning — then memorization strategies may suffice. But if the goal is transfer, flexible thinking, and application in new contexts, then deep learning strategies are essential.
Mathematics mastery does not come from choosing between understanding or fluency.
It comes from weaving them together.

Evidence-based mathematics
Research consistently shows that conceptual understanding, procedural fluency, and real-world application work best as a team. When students understand the why, they remember the how more flexibly. When procedures become automatic, their cognitive energy is freed for deeper reasoning and more complex problem solving (Mitchell, 2025).
Empower All Math Minds operationalizes that research.
Through dynamic strategic games, thoughtfully designed lesson guides that incorporate surface, deep, and transfer strategies, and carefully selected manipulatives, we transform classrooms into spaces where:
Understanding strengthens fluency
Fluency supports reasoning
Reasoning builds confidence
Confidence fuels persistence
Persistence creates mastery
This is not a pendulum swing.
It is an integrated design for mathematical proficiency.
The Five Pillars Mathematical Empowerment
True mathematical mastery is not built on memorized algorithms alone or open-ended exploration alone. It is constructed through five interwoven capacities that together form mathematical proficiency. Empower All Math Minds develops these capacities intentionally, systematically, and joyfully.
Pillar 1: Strategic Games and Manipulatives Develop Strategic Thinkers
Our classroom math games are intentionally designed to develop strategic thinkers. Through math games and hands-on manipulatives, students formulate problems, represent relationships, and evaluate multiple solution strategies.
In an atmosphere of play, students naturally support one another. They compare approaches, ask questions, and refine thinking together. These fun math games create a space where strategic competence grows through collaboration rather than correction.
Strategic thinkers:
Compare and evaluate alternative solution methods
Ask peers about strategies and reflect on differences
Recognize when an answer does not make sense and try another approach
Represent problems using models, diagrams, equations, and words
Manipulatives make mathematical structure visible. Games make strategic thinking active.
Pillar 2: Flexible Fluency Through Play and Application
As students engage in a variety of math games and rich classroom activities, they apply mathematics in multiple ways. This repeated, varied practice naturally builds flexibility and procedural fluency.
Strategic games deepen conceptual understanding while strengthening automaticity. When students set up mathematical relationships within games, they rehearse structure and computation at the same time. The play makes it engaging. The repetition makes it stick.
Our fun math games provide meaningful math help by embedding fluency inside real thinking—not isolated drills.
Fluent students:
Perform computations accurately and efficiently
Recognize when estimation is appropriate
Connect student-generated strategies to efficient procedures
Use procedures flexibly in unfamiliar contexts
As fluency strengthens, mental energy is freed for deeper reasoning.
Pillar 3: Deep Concept Builders
Manipulatives support deeper thinking by allowing students to see, build, and test mathematical relationships. Instead of memorizing disconnected procedures, students develop conceptual understanding through active exploration.
In our math games, manipulatives are not add-ons—they are thinking tools. They help students connect numbers, operations, and representations in ways that strengthen long-term retention and transfer.
Concept builders:
Represent mathematical relationships in multiple ways
Explain ideas verbally, visually, symbolically, and physically
Recognize connections across problems and grade levels
Apply concepts in real-world situations
When understanding is deep, retention is stronger and procedures become automatic chunks rather than mechanical steps to follow.
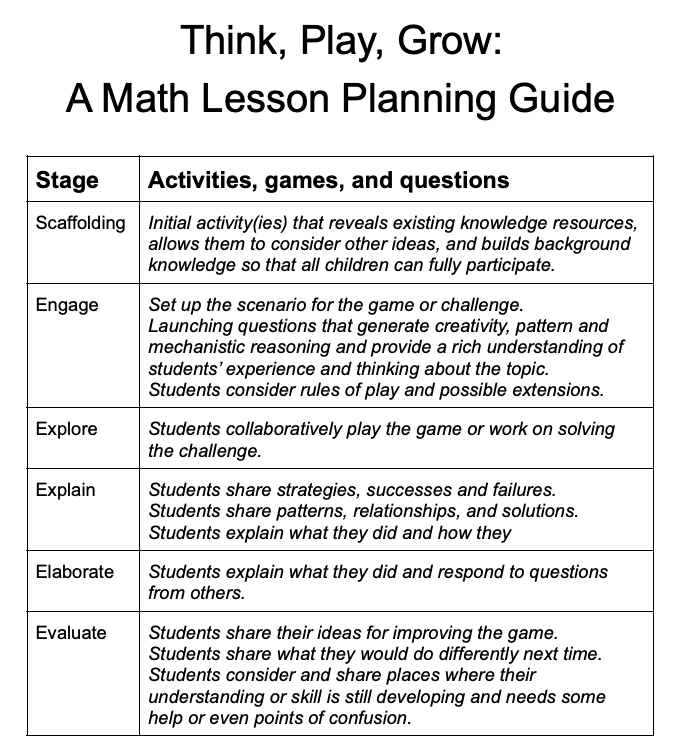
Pillar 4: Lesson Plans That Cultivate Adaptive Reasoning
Our lesson guides, often used as classroom lesson plans, are designed to activate and build on background knowledge. Each lesson plan includes purposeful questioning before, during, and after play.
Debrief discussions following math games extract student thinking, invite evaluation, and encourage reasoning and revision. Students explain strategies, compare solutions, and refine understanding.
These lesson plans transform classroom math games into structured opportunities for deeper learning.
Adaptive reasoners:
Provide informal and formal justifications
Analyze and correct errors
Reflect on why they changed strategies
Apply learning from one context to another
In these classrooms, explanation and evaluation matter as much as answers.
Pillar 5: Games Develop Mathematical Believers
Math games build more than skills—they build belief.
Through consistent engagement in fun math games, students develop fluency and confidence in their ability to figure things out. They learn to try new strategies, revise mistakes, and persist through challenges. Play reduces anxiety while increasing competence. Students receive meaningful math help through collaborative problem-solving rather than passive correction.
Mathematics becomes a space of creativity, problem-solving, and agency, not avoidance.
Mathematical believers:
Persevere through challenge
Believe they are capable of figuring it out
Try multiple strategies
Revise mistakes independently
When this pillar is strong, helplessness dissolves. Confidence grows from authentic achievement.
When the Five Pillars Work Together
Strategic thinking strengthens fluency.
Fluency supports reasoning.
Conceptual understanding protects against forgetting.
Adaptive reasoning deepens learning.
Productive disposition fuels persistence.
Empower All Math Minds does not separate skills from understanding. We design learning experiences where strategic games, manipulatives, discussion, distributed practice, and reflection activate all five pillars simultaneously.
This is how mathematical mastery becomes the norm — not the exception.
Gaming Up for Math Transformation
Real educational change goes beyond introducing a new teaching strategy. It requires daily tools that help teachers bring innovation to life—lesson plans, interactive games, and meaningful resources. Our shop provides everything needed to support a shift toward dynamic, student-centered mathematics mindset classrooms.
In-Person Support for Real Math Transformation
Unlocking the future of learning requires more than innovative resources—it takes in-person support tailored to your school’s unique context. We help educators navigate challenges, adapt to system-specific needs, and lead the tough conversations that drive real change. Let us guide your journey toward a new era of mathematics excellence.
-
Requests for webinar trainings are welcome.
-
Submissions for game or challenge requests for specific concepts are welcome.
Empower All Math Minds is committed to taking actions that have a positive impact on society and school environments.
References
Hattie, J. A., & Donoghue, G. M. (2016). Learning strategies: A synthesis and conceptual model. npj Science of Learning, 1(1), 1-13.
Mitchell, A. S. (2025, August 25). Conceptual Understanding, Procedural Fluency, & Application... Carnegielearning.com; Carnegie Learning Inc. https://www.carnegielearning.com/blog/conceptual-understanding
National Research Council. 2001. Adding It Up: Helping Children Learn Mathematics. Washington, DC: The National Academies Press.